Kamm'sche Kreis
Der Kamm'sche Kreis wird ausführlich diskutiert in: Spiegel, Bernt: Die obere Hälfte des Motorrades. Das wird hier noch nachgetragen. Die folgende Kurzversion stammt von http://www.ttatwest.de/tips/kam/k_kreis.htm
Der Kamm'sche Kreis stellt die mögliche Kraftübertragung als Vektor
in einem Diagram mit Quer- und Längskräften dar.
Die Fliehkraft (Zentrifugalkraft) ist eine Kraft, die einen bewegten Körper von einem Zentrum nach aussen fort-
zuziehen versucht. Sie ist eine Trägheitskraft, d.h., sie entsteht erst, wenn der Körper durch eine andere Kraft
(Zentripetalkraft) aus seiner geradlinigen Bewegung herausgezwungen wird und verschwindet mit dem Auf-
hören dieses Zwangs.
Bei jedem Lenkmanöver während der Fahrt treten Fliehkräfte auf, die durch die Seitenführungskraft der Räder
abgebaut werden. Dadurch wird verhindert, dass das Fahrzeug in einer Kurve von der Fahrbahn abkommt.
Die Fliehkraft steigt bei einer Verdoppelung der Geschwindigkeit um den vierfachen Wert an!
Beispiel: durch eine Erhöhung der Geschwindigkeit, mit der man in eine Kurve fährt, von 50 auf 75 km/h werden die ab-
zubauenden Fliehkräfte an den Reifen verdoppelt.
Jeder Reifen kann nur eine bestimmte maximale Beschleunigungskraft und eine bestimmte maximale Seiten-
führungskraft übertragen. Wichtig ist zu wissen, dass Beschleunigungskräfte und Seitenführungskräfte in direktem Zusammenhang stehen (Positive Beschleunigung = Gasgeben - negative Beschleunigung = Bremsen).
Das bedeutet, dass beim Auftreten beider Kräfte, die einzelne Kraft nicht mehr so wirken kann, wie bei alleini-
gem Auftreten.
Diese physikalischen Gegebenheiten kann man auch vereinfacht als Grafik darstellen -
im sogenannten "Kamm'schen Kreis".
Fig.1
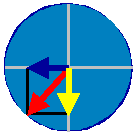
|
Fig.2
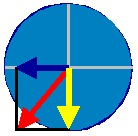
|
60%
der max. Seitenführungskraft + 70% Bremswirkung;
reicht
gerade noch um einen Abflug zu verhindern!
|
80%
der max. Seitenführungskraft + Vollbremsung.
Der
Fahrer fährt die Kurve sehr schnell an
und
muss eine Vollbremsung machen:
Abflug
!!!!
|
Fig.3
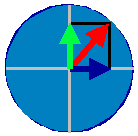
|
Fig.4
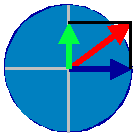
|
60%
der max. Seitenführungskraft + 70% Beschleunigung.
reicht
gerade noch!
Ein
weiteres Beschleunigen würde das Aus bedeuten.
|
100%
der max. Seitenführungskraft + 70% Beschleunigung.
Der
Fahrer fährt die Kurve sehr schnell an
und
beschleunigt noch:
Abflug
!!!!
|
Blauer
Pfeil = Seitenführungskraft
Grüner
Pfeil = Beschleunigungskraft
Gelber
Pfei l = negative Beschleunigung
Roter
Pfeil = Gesamtsumme der übertragenen
Kräfte
Der Durchmesser des Kreises variiert natürlich abhängig von den Fahrbahnbedingungen.
Bei Regen oder Glatteis wird der Kreis kleiner!
Mittlerweile weiß jeder, dass bei blockierten Rädern ein wirksames Bremsen nicht mehr möglich ist.
Ebenso verhält es sich, wenn man bei entsprechend hoher Geschwindigkeit in einer Kurve eine Vollbremsung
durchführt: Auto mit Fahrer werden dabei unfreiwillig die Straße verlassen (Fig.2).
Ein Reifen, der alle seine Haltekräfte für die Seitenführung in der Kurve verbraucht, hat keine Reserven mehr
für eine positive oder negative Beschleunigung übrig.
Wer also eine Kurve mit maximal möglicher Geschwindigkeit fährt, sollte weder bremsen noch Gas geben (Fig.4).
Eine negative Beschleunigung wird auch erreicht, wenn plötzlich das Gas zurückgenommen wird. Wird die
gesamte Kraft für die Beschleunigung genutzt (Pfeil steht senkrecht), dann kann der Reifen keine Seitenkräfte
mehr übertragen = "Abflug".
Wird dagegen die gesamte Kraft für die Seitenführung benötigt (Pfeil steht waagerecht), dann führt jedes Gas-
geben oder Bremsen zum "Abflug".
Dazwischen können sowohl Seiten- als auch Längskräft übertragen werden, die sich vektoriell addieren.
Nach dem Pythagoras gilt damit:
(Reibungskraft)² = (Längskraft)² + (Seitenführungskraft)²
Ein allradgetriebenes Fahrzeug hat beim Beschleunigen in Kurven etwas größere Sicherheitsreserven, da die
Kräfte statt auf zwei, auf vier Räder übertragen werden.



