|
|
|
|
Konstruiere ein ganz einfaches quantitatives Modell einer Heizung und schaue, wie sich das Modell verhält! |
Was mit dem Computer geht, kan man ja - im Prinzip - auch auf einem Blatt Papier durchspielen. Man ist dann quasi ein Modell des Computers - wie das Modell des Künsters quasi invers ein Modell seines Bildes ist. Man kann beispielsweise so verfahren:
Eine Heizung braucht natürlich einen Sollwert und einen abweichenden Ist-Wert, damit überhaupt etwas passiert. |
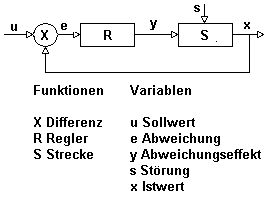
Die Temperatur wird jede Stunde in Grad C gemessen, x ist eine ganze Zahl pro Stunde. u wird eingestellt. e wird als Differenz u-x berechnet. R enthält folgende Funktion: Wenn e grösser als 0 ist, wird geheizt, also der Brenner eingeschaltet.Wenn e kleiner als 0 ist, wird der Brenner ausgeschaltet. Es kann in diesem Modell also nur geheizt oder nicht geheizt werden, nicht verschieden stark oder verschieden lang. y ist also 1 oder 0. Wenn geheizt wird (y=1), steigt die Temperatur innerhalb einer Stunde um 3 Grad. Unabhängig vom Heizen fällt die Temperatur pro Stunde um 1 Grad.
Ich beginne mit: u=20, x=14
Wenn die Heizung etwas weniger unmittelbar funktionert, steigt die Temperatur erst nach 3 Stunde um 3 Grad, dann verändern sich die Werte mit desselben Anfangswerten wie folgt Ich beginne mit: u=20, x=14
|
Beide Beispiele sind ganz primitiv, zeigen aber zusammen, wie verschieden das Verhalten bei kleinen Aenderungen wird. Wenn eine Verzögerung berücksichtig wird, findet das System seinen Sollwert viel schlechter. Die Verzögerung kann natürlich durch weitere Mechanismen kompensiert werden. Vor allem kann eine Heizung ja bei verschiedenen Abweichungen x von u verschiedene e produzieren. Umgekehrt besteht Regelungsbedarf naürlich vor allem, weil die Störung nicht konstant ist, also weil die Aussentemperatur so schwankt, dass die Innentemperatur nicht konstant abnimmt. Spielen Sie das Spiel, indem Sie bei beliebigen Zeitpunkten die Aussentemperatur, und als Folge davon den Wert von x verändern! |
|
|