Hyper-Lexikon: Dialogische Logik

Dialogische Logik [ zurück ] [ Index ] [ Literatur-Index ] [ Die Hyper-Bibliothek ] [ Mehr zum Thema ]

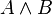
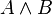
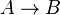
Die dialogische Logik (englisch: game semantics) ist ein von K. Lorenz und Paul Lorenzen entwickelter spieltheoretischer, semantiknaher Ansatz, Arithmetik und Logik als Dialogspiele zu konstruieren. Die Motivation ist eine im Vergleich zum Ableiten in Logikkalkülen nähere Orientierung am menschlichen Argumentieren.

Wahr heisst eine aus logischen Zeichen zusammengesetzte Aussage, wenn sie sich im Dialog immer gewinnen lässt. Formal wahr wird eine solche Aussage genannt, wenn sie stets gewonnen werden kann, ohne in einen Dialog über die Primaussagen (Elementarsätze) einzutreten.

Rahmenregeln

Der Proponent beginnt den Dialog, indem er eine mit logischen Zeichen verknüpfte Aussage äußert.
Die Dialogpartner sind abwechselnd am Zug.
Das weitere Vorgehen besteht aus Angriffen und Verteidigungen.
Ein Angriff stellt ein Recht dar, eine noch angreifbare Aussage des Gegners anzugreifen.
Eine Verteidigung ist die Pflicht, sich auf eine angegriffene Aussage zu verteidigen, spätestens wenn man selber nicht mehr angreifen darf.
Die Angriffe und Verteidigungen sind in den Partikelregeln normiert.
Der Proponent hat gewonnen, wenn er eine angegriffene Elementaraussage verteidigt hat oder wenn der Opponent eine angegriffene Elementaraussage nicht verteidigt.

Eine Besonderheit stellt die folgende effektive Rahmenregel dar. Sie lautet:

Die jeweils zuletzt entstandene Verteidigungspflicht ist zuerst zu erfüllen. Da es gegen eine Verneinung keine Verteidigung gibt (s.u.), entfällt mit jeder erfolgten Verneinung die Möglichkeit für den Gegenspieler, Aussagen zu verteidigen, die vor der Verneinung angegriffen wurden.

Wenn die effektive Rahmenregel gilt, ist die dialogische Logik ein Modell der intuitionistischen Logik. Wenn sie nicht gilt, also wenn jede Aussage zu jedem Zeitpunkt des Dialogs verteidigt werden kann, ist sie ein Modell der klassischen Logik. Intuitionistische (effektive) Logik und klassisch-zweiwertige Logik lassen sich also durch Verwendung oder Wegnahme der effektiven Rahmenregel ineinander überführen.

Angriffs- und Verteidigungsregeln für die logischen Operatoren

Hier sind die Angriffs- und Verteidigungsregeln der dialogischen Logik aufgelistet:

Junktoren	Angriff	Verteidigung
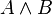$A \land B$	$L ?$	$A$	(und)
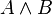$A \land B$	$R ?$	$B$	(und)
$A \lor B$	$?$	$A$ / $B$	(oder)
$\neg A$	$A ?$	...	(nicht)
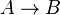$A\rightarrow B$	$A ?$	$B$	(wenn–dann)

Die letztgenannte Junktor-Operation wenn-dann wird hier Subjunktion, sonst meist Implikation genannt.

Quantoren	Angriff	Verteidigung
$\bigwedge x\;A(x)$	$n ?$	$A (n)$
$\bigvee x\;A(x)$	$?$	$A (n)$

Quantorzeichen: 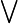$\bigvee$ (Einsquantor: "für ein") bzw. 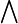$\bigwedge$ (Allquantor: "für alle")

Beispiele

Hier als einfaches Beispiel ein Dialog um $a \rightarrow a$ . Die Aussage ist formal logisch wahr:

$O$	$P$
	$a \rightarrow a$
$a ?$		(Die Subjunktionbehauptung wird angegriffen nach der Subjunktionsregel: Die voranstehende Pa wird behauptet.)
	$a$	(Als Verteidigung wird die nachstehende Pa genannt, dies ist gleichzeitig auch eine Übernahme des $a$ der vorigen Zeile.)

$P$ kann den Dialog immer gewinnen, denn er kann $a$ übernehmen.

Im folgenden weitere Beispiele, zunächst für den klassisch und intuitionistisch wahren Satz $A\rightarrow \neg\neg A$ , dann für den nur klassisch wahren Satz $\neg\neg A\rightarrow A$ .

Es wird hier auch bei Verteidigungen angegeben, gegen welchen Angriff sie sich richten. „1!“ heißt also „verteidigt sich gegen den Angriff unter 1“, und „1?“ bedeutet „greift die Aussage unter 1 an“. Klammern bezeichnen Züge, die unter Einhaltung der effektiven Rahmenregel nicht möglich sind.

		$O$		$P$
1.				$A \rightarrow\neg\neg A$
2.	$1?$	$A$	$2!$	$\neg\neg A$
3	$2?$	$\neg A$	$3?$	$A$
4	$3?$		$2?$

$P$ stellt in Schritt 3 eine Primaussage, nämlich $A$ auf, die $O$ in Schritt 2 schon behauptet hat. Nach den Regeln ist der Dialog damit für $P$ gewonnen.

Ganz anders sieht es für $\neg\neg A \rightarrow A$ aus:

		$O$		$P$
1.				$\neg\neg A\rightarrow A$
2.	$1?$	$\neg\neg A$	$2?$	$\neg A$
3.	$2?$	$A$	( $2!$ )	$A$

Im letzten Schritt verteidigt $P$ die Aussage unter 1, die $O$ in Schritt 2 angegriffen hat. Da $O$ nach Schritt 2 noch Aussagen von $P$ angegriffen hat, ist die Verteidigung nur in der klassischen Logik möglich, nicht aber in der intuitionistischen Logik. Auch ein anderer Spielverlauf hilft nicht:

		$O$		$P$
1.				$\neg\neg A\rightarrow A$
2.	$1?$	$\neg\neg A$	$2!$	$A$
3.	$2?$		$2?$	$\neg A$
4.	$3?$	$A$	( $3!$ )	$A$

$O$ greift in Schritt 3 die Primaussage $A$ an. Obwohl er sie in Schritt 4 selbst einräumt, kann P sich nicht mehr gegen diesen Angriff verteidigen, da inzwischen ein weiterer Angriff erfolgt ist.

Da der Proponent keinen Spielverlauf erzwingen kann, wo er unter Einhaltung der effektiven Rahmenregel gewinnt, ist die Aussage $\neg\neg A\rightarrow A$ in der intuitionistischen Logik nicht zu beweisen. In der klassischen Logik hingegen gilt sie, wie die Beispiele zeigen.

Anwendungen

Interessant sind die speziellen Effekte, die bei der (intuitionistischen) Interpretation des Subjunktors ( $\rightarrow$ ) auftreten: Während des Dialogs sind auch nicht wahrheitsdefinite (eine Aussage ist entweder wahr oder falsch) Aussagen erlaubt. Der Wahrheitswert der Aussagen kann in einem Schwebezustand belassen bleiben. Bei der effektiven Rahmenregel wird der Satz vom ausgeschlossenen Dritten nicht voraussetzt. Erst bei Abschluss des Dialogs steht der Wahrheitswert der Gesamtaussage fest. Carl Friedrich von Weizsäcker hat einige dieser Regeln für die Interpretation der Quantenphysik durch zeitliche Logik aufgenommen. (Ein berühmtes vereinfachtes Beispiel der Quantenlogik von C.F. v. Weizsäcker: Während wir überlegen, ob der Mond untergeht oder nicht, geht er unter.)

Weitere Anwendungen ergeben sich für die Argumentationstheorie, da die dialogische Logik im Verlauf des Dialogs aufzeigt, wer wann Beweislast für Tatsachenbehauptungen in Form von Elementaraussagen übernimmt.

[]