|
Der Ausdruck Logik wird in beliebigen Zusammenhängen für beliebiges verwendet, was mit dem, was ich als Logik bezeichne gar nichts zu tun hat.
|
Als Fuzzylogik bezeichne ich - in Anlehnung an eine Konvention - ein Verfahren, ... (eine schlaue Übersetzung lautet: "unscharfe Theorie"), welche in der Mustererkennung zur „präzisen Erfassung des Unpräzisen“ (Zadeh) entwickelt wurde, sodann der Modellierung von Unschärfe von umgangssprachlichen Beschreibungen von Systemen dienen sollte, heute aber überwiegend in angewandten Bereichen wie etwa der Regelungstechnik eine Rolle spielt. Als Verallgemeinerung der zweiwertigen Booleschen Logik erlaubt sie beispielsweise die Ausprägung einer Eigenschaft – wie sie die sogenannten Heckenausdrücke „ein bisschen“, „ziemlich“, „stark“ oder „sehr“ der natürlichen Sprache zur Verstärkung oder Abschwächung eines Prädikats bereitstellen – als Zugehörigkeitsgrad numerisch zu erfassen und damit die Unschärfe (Fuzziness) eines sprachlichen Ausdrucks mathematisch präzise zu modellieren. Die Fuzzylogik basiert auf den unscharfen (fuzzy) Mengen (Fuzzy-Sets). Dabei wird die Menge nicht wie bisher durch die Objekte definiert, die Elemente dieser Menge sind (oder nicht sind), sondern über den Grad ihrer Zugehörigkeit zu dieser Menge. Das geschieht durch Zugehörigkeitsfunktionen, die jedem Element einen numerischen Wert als Zugehörigkeitsgrad zuordnen. Die so eingeführten neuen Mengenoperationen definieren die Operationen eines zugehörigen Logikkalküls, das die Modellierung von Inferenzprozessen erlaubt.
Eine praktische Bedeutung - die mit Logik aber wenig zu tun hat - liegt darin, dass Datenbanken auch unbestimmte, fehlende oder sogar widersprüchliche Informationen enthalten können.
Fuzzy-Logik (englisch: fuzzy = ungenau, verschwommen, unscharf) ist eine Theorie, eine Verallgemeinerung der zweiwertigen Booleschen Logik, die vor allem für die Darstellung menschlichen Wissens und menschlicher Überlegung zur Verarbeitung in Computern entwickelt wurde.
Fuzzy-Computersysteme verarbeiten gegenüber herkömmlichen Systemen nicht nur Werte wie JA und NEIN (bzw. AN und AUS oder 1 und 0), sondern zusätzlich auch Zwischenwerte (Wahrheitswerte) zwischen WAHR (=1) und FALSCH (=0) z.B. 0,5, sodass damit auch unscharfe Mengenabgrenzungen mathematisch behandelt werden können, die sich aus Kombinationen von JA und NEIN mit ZIEMLICH, SEHR und ZIEMLICH WAHRSCHEINLICH ergeben. Damit können fuzzylogikunterstützte Programme "menschlicher denken" als übliche Computer.
Die Fuzzy-Set-Theorie, also die unscharfe Mengenlehre, wurde bereits 1965 von L. A. Zadeh, Professor für Computerwissenschaften an der Universität von Berkeley, USA, entwickelt. Die Grundlagen dazu wurden jedoch schon früher von dem polnischen Logiker Jan Lukasiewicz entwickelt, der zur Beschreibung des Wahrheitswertes einer logischen Aussage Zahlen aus dem reellen Einheitsintervall [0, 1] (die reellen Zahlen zwischen 0 und 1 einschließlich der Ränder) verwendete. Heute wird die Fuzzy-Logik bzw. Fuzzy-Control vorwiegend bei der Steuerung von Maschinen und Robotern oder auch handelsüblichen Haushaltsgeräten verwendet.
Fuzzy-Logik wird sehr breitbandig in unterschiedlichsten Bereichen eingesetzt. Anwendungen finden sich in der Automatisierungstechnik, der Betriebswirtschaft, der Medizintechnik, der Konsumelektronik, der Automobiltechnik usw. Nützlich ist die Verwendung von Fuzzy Logik oft dann, wenn keine mathematische Beschreibung eines Sachverhaltes oder Problems vorliegt, sondern nur eine umgangssprachliche, d.h. verbale. Dann kann aus linguistisch formulierten Sätzen und Regeln mittels Fuzzy-Logik eine solche mathematische Beschreibung gewonnen werden, die in Rechnersystemen genutzt werden kann.
In einer typischen Anwendung werden Waschmaschinen so programmiert, dass sie je nach Verschmutzung der Wäsche ihre Waschmittelmenge regeln. Ausgangspunkt ist die Überlegung, dass es nicht möglich ist, den Verschmutzungsgrad für Kleidung eindeutig zu bestimmen. Beispielsweise gibt es keine Definition eines "Verschmutzungsgrads 55%". Da aber die Waschmittelmenge dennoch auf einen festen Wert eingestellt werden muss, benötigt man hier eine Logik, die mit unscharfen Begriffen wie leicht verschmutzt oder stark verdreckt umgehen kann. Die Fuzzy-Logik "übersetzt" die Aussagen zur Wäscheverschmutzung in eine fest definierte Waschmittelmenge. Beispielsweise wird "leicht verschmutzt" in 23 g Waschmittel und "stark verdreckt" in 65 g Waschmittel umgesetzt. Entscheidend ist, dass hinter dieser "Logik" keine eindeutige mathematische (lineare) Funktion zu finden ist. Vielmehr müssen die maßgebenden Werte ("23 g" oder "65 g") aus Erfahrungen, Beobachtungen und empirischen Untersuchungen gewonnen werden.
Weitere Anwendungen sind die Regelung von U-Bahnen, die Steuerung automatischer Getriebe in Automobilen, Alarmsysteme für die Anästhesie, Zwischenfrequenzfilter in Radios, ABS für Automobile, Brandmeldetechnik, die Prognose des Energieverbrauchs bei Energieversorgern etc.
Grundlage der Fuzzy-Logik sind die so genannten unscharfen Mengen. Im Gegensatz zu traditionellen Mengen (im Kontext der Fuzzy-Logik auch scharfe Mengen genannt), in denen ein Element in einer Grundmenge entweder enthalten oder nicht enthalten sein kann, kann ein Element in einer unscharfen Menge auch ein wenig enthalten sein. Der Grad an Zugehörigkeit wird meist durch eine Zugehörigkeitsfunktion (Fuzzyfunktion) µ beschrieben, die den Elementen einer Grundmenge eine reelle Zahl zwischen 0 und 1 zuordnet.
Auch auf unscharfen Mengen sind Operationen wie auf scharfen Mengen möglich, wie z. B. Durchschnitt (UND), Vereinigung (ODER) und Komplement (NICHT). Zur Modellierung dieser Operationen bedient man sich der Funktionsklassen T-Norm, S-Norm und Negation.
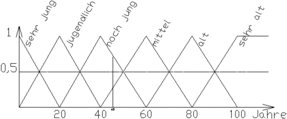Fuzzyfunktion für das Alter eines Menschen
Die Zugehörigkeitsfunktionen sind die "Fuzzyfunktionen". Ein Beispiel dafür ist eine Fuzzyfunktion für das Alter eines Menschen. Sie besteht aus mehreren dachförmigen Dreiecken für verschiedene Altersbereiche.
Jedes Dreieck deckt einen Bereich von mehreren Jahren des Menschenalters ab. Ein Mensch mit 45 Jahren hätte so die Eigenschaften: "noch jung" mit der Wertung 0,75 (das ist noch relativ viel), "mittleres Alter" mit der Wertung 0,25 (das ist ein bisschen) und von den übrigen Funktionen nichts. Anders ausgedrückt: mit 45 ist man ziemlich viel "noch jung" und ein bisschen "mittelalt". - Man gewinnt solche Fuzzyfunktionen aus Erfahrung oder indem man Experten des betreffenden Gebiets befragt, wobei bei dieser Frage wohl jeder ein "Experte" ist.