Als imaginäre Zahl bezeichne ich eine Zahl, deren Quadrat eine nichtpositive reelle Zahl ist. Sie ist imaginär in dem Sinne, dass es dazu keine Anschauung gibt. Es gibt aber Rechnungsverfahren, in welchen die imaginären Zahlen als Konstrukte verwendet werden. In den imaginären Zahlen lassen sich Gleichungen lösen, die keine reellen Lösungen haben können. Zum Beispiel hat die Gleichung x2 − 4 = 0 als Lösung zwei reelle Zahlen, nämlich 2 und −2. Aber die Gleichung x2 + 4 = 0 kann keine reelle Lösung haben, da Quadrate reeller Zahlen niemals negativ sind, sodass es keine reelle Zahl gibt, deren Quadrat −4 wäre. Die Lösung dieser Gleichung sind zwei imaginäre Zahlen, + 2 i und − 2 i. Ein negatives Quadrat gibt es - in der Imagination - nicht, ich kann es nicht zeichnen. a2 kann ich als Quadrat misverstehen. Im gleichen Sinn ist dann a3 ein Würfel. In dieser "imaginären" Vorstellung gibt es aber kein a4. a4 kann ich mir aber ganz leicht vorstellen, wenn a viermal mit sich selbst multppliziere. Ich habe beispielsweise 4 Äpfel und jemand gibt mir für jeden Apfel den ich ihm gebe, 4 Äpfel. Dann habe ich 16 Äpfel, also kein Quadrat und keinen Würfel. Deshalb brauche ich keine imaginäre Vorstellung für a4.

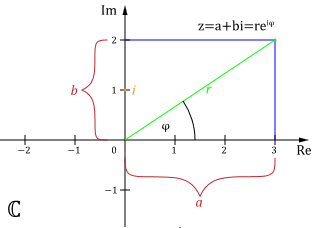
Gaussebene Bildquelle: Wikipedia

Eine primitive Veranschaulichung der imaginären Zahlen basiert auf der sogenannten Gaussebene, in welcher Zahlen nicht auf einer Reihe, sondern auf einer - imaginären - Fläche liegen.

Die Bezeichnung „imaginär“ wurde zuerst 1637 von R. Descartes benutzt, allerdings für nichtreelle Lösungen von algebraischen Gleichungen.

Der Ursprung der Theorie der imaginären Zahlen geht auf die italienischen Mathematiker Gerolamo Cardano und Rafael Bombelli bis ins 16. Jahrhundert zurück. Die Einführung der imaginären Einheit i als neue Zahl wird Leonhard Euler zugeschrieben. Diese Bezeichnung wurde vermutlich von Gerolamo Cardano geprägt. Nach seiner Ansicht konnten solche Zahlen nicht existieren, sie konnten also nur imaginär (eingebildet) sein.

imaginäre Menge
Der so konstruierte Zahlenbereich der komplexen Zahlen bildet einen Körper und hat eine Reihe vorteilhafter Eigenschaften, die sich in vielen Bereichen der Natur- und Ingenieurwissenschaften als äußerst nützlich erwiesen haben. Einer der Gründe für diese positiven Eigenschaften ist die algebraische Abgeschlossenheit der komplexen Zahlen. Dies bedeutet, dass jede algebraische Gleichung vom Grad größer Null über den komplexen Zahlen eine Lösung besitzt, was für reelle Zahlen nicht gilt. Diese Eigenschaft ist der Inhalt des Fundamentalsatzes der Algebra. Ein weiterer Grund ist ein Zusammenhang zwischen trigonometrischen Funktionen und der Exponentialfunktion, der über die komplexen Zahlen hergestellt werden kann. Ferner ist jede auf einer offenen Menge einmal komplex differenzierbare Funktion dort von selbst beliebig oft differenzierbar, anders als in der Analysis der reellen Zahlen. Die Eigenschaften von Funktionen mit komplexen Argumenten sind Gegenstand der Funktionentheorie, auch komplexe Analysis genannt.