======Das Wort „quantitas“ lässt sich auf zwei Arten ins Deutsche übersetzen, nämlich als „Größe“, im Sinn einer physikalischen Größe, oder aber als „Menge“. Der Name „Bewegungsmenge“ träfe das was Descartes meinte, vor allem aber auch die moderne Auffassung von ! p , viel besser.=========== Die "Mengenartige Grösse" wurde im Karlsruher Physikkurs als Basisgrössen eingeführt. Eine physikalische Grösse kann nicht mengenartig sein, was immer mengenartig bedeuten soll. Eine Menge hat im umgangssprachlichen Sinn eine Grösse, ich kann etwa von einer grossen Menge sprechen. Ein Fluidum ist eine Sache, keine Grösse. Die Physiker haben ein Sprachproblem mit Homonymen wie Grösse und Energie. Sie erfinden unsinnige Kunstwörter.   2.1 Mengenartige Grössen (aus Herrmann, F.: KPK) Es gibt eine Klasse physikalischer Grössen, von denen man sich besonders leicht eine Anschauung bilden kann. Wir nennen sie mengenartige Grössen. Zu ihnen gehören Masse, Energie, elektrische Ladung, Stoffmenge, Impuls, Drehimpuls, Entropie und andere. Man darf sich jede dieser Grössen wie eine Art Stoff oder wie ein Fluidum vorstellen. Mit „vorstellen“ ist gemeint, dass man physikalisch korrekt mit ihnen umgeht, wenn man über sie spricht wie man über einen Stoff spricht. Man darf dasselbe Vokabular verwenden, das in der Umgangssprache benutzt wird, um Substanzen zu bilanzieren. Ein Kennzeichen dafür, dass eine Größe X mengenartig ist, ist ihr Auftreten in einer Kontinuitätsgleichung: dX/dt = IX + ΣX Diese Gleichung macht eine Aussage über ein bestimmtes Raumgebiet. Man kann der Kontinuitätsgleichung eine anschauliche Deutung geben, indem man IX als die Stärke eines Stroms durch die Oberfläche des Bereichs interpretiert (Herrmann 1986). Die Änderung des Wertes von X hat demnach zwei Ursachen: Zum einen die Erzeugung bzw. Vernichtung von X im Innern des Gebiets und zum anderen einen Strom durch die Oberfläche. 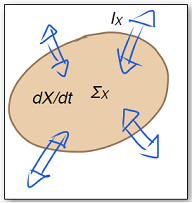Hinweis: Damit wird explizit eine gewollte Verbindung zur Umgangssprache angezeigt, die aber in keiner Weise reflektiert wird, sondern jene falschen Vorstellungen hervorruft, die der DGP dem Kurs anlastet   dX/dt stellt die zeitliche Änderung des Werts von X im Innern des Raumgebiets dar. Auch ΣX bezieht sich auf das Innere des Gebiets. Dieser Term gibt an, wie viel der Menge X dort pro Zeiteinheit erzeugt bzw. vernichtet wird. IX dagegen ist eine Größe, deren Wert sich auf die Oberfläche des Raumgebiets bezieht. Bildquelle: KPK

Als "mengenartige Grösse" bezeichne ich - in Anlehung an ein schlecht gewähltes Wort des KPK - den "Stoff" oder die "Sache", der in der Physik "behandelt" wird. Mit Behandeln meine ich messen, davon ist aber im KPK nicht die Rede.

Die mengenartige Grösse ist ein Abstraktum, dessen Grösse sich durch Zufluss und Abfluss verändert, das aber auch Entstehen oder Vergehen kann.

Anschauliches Bild:
Auf einer Insel leben Vögel. Es werden mehr, wenn neue Vögel durch Geburt oder Zuwanderung dazukommen, und weniger, wenn Vögel sterben oder wegziehen.
Die Grösse hat einen jeweiligen Wert, der sich auf einen Raumbereich bezieht.

Energie soll man sich - im Rahmen des KPKs - genau so vorstellen.

Der KPK kennt folgende mengenartige Basisgrössen:
Masse
Energie
Impuls
elektrische Ladung
Entropie
Stoffmenge

Zu jeder dieser Grössen kann man eine Dichte erklären, und zu jeder von ihnen gibt es einen Strom mit einer Stromstärke und einer Stromdichte.

Daraus folgen zwei Besonderheiten des KPK:
In der Mechanik geht es von Anfang an um den Impuls und seine Ströme.
In der vormaligen Wärmelehre geht es von Anfang an um die Entropie und ihre Ströme.

Daraus folgen zwei Besonderheiten des KPK:
In der Mechanik geht es von Anfang an um den Impuls und seine Ströme.
In der vormaligen Wärmelehre geht es von Anfang an um die Entropie und ihre Ströme.

Der KPK führt zu einer einfacheren Darstellung der klassischen Physik. Eine Reihe von schwierigen Konzepten, die früher eine gewisse Existenzberechtigung hatten, sind aus heutiger Sicht überflüssig. Hierzu gehört der Begriff der Energieform, und damit insbesondere die Begriffe Wärme und Arbeit. (KPK. Begleittext für Lehrer)

??? Dass sie sich in den hier vorgeschlagenen Kurs auf natürliche Art einordnen lässt, liegt daran, dass wir zu ihrer Beschreibung eine Größe in den Physikunterricht einführen, die traditionell darin nicht vorkommt: das Shannonsche Maß für die Datenmenge. ???

Nichtmengenartigen Grössen sind die elektrische Feldstärke oder die Temperatur. (Bei ihnen hat die Frage nach der Erhaltung keinen Sinn.)

Die mengenartigen Grössen werden auch als extensive Grössen bezeichnet.
Eine Teilmenge davon sind Erhaltungsgrössen. Sie werden nur durch Zu- und Abfluss verändert.

Die Forderung, dass jede mengenartige Größe einer Kontinuitätsgleichung genügt, impliziert einige einfache Merkmale solcher Größen: